Lecture meeting times: Section J 2:00-2:50 in CoC 16
Instructor: Sal Barone
Office: Skiles 013 and https://gatech.zoom.us/my/sbarone7
Office hours: Monday and Friday at 12pm (and by appointment, email me) - all office hours are in-person, or streamed/recorded by request.
email: sbarone at math.gatech.edu
Links for Online Instruction
MATLAB Materials
Blank Lecture Notes
Annotated Lecture Notes for current semester
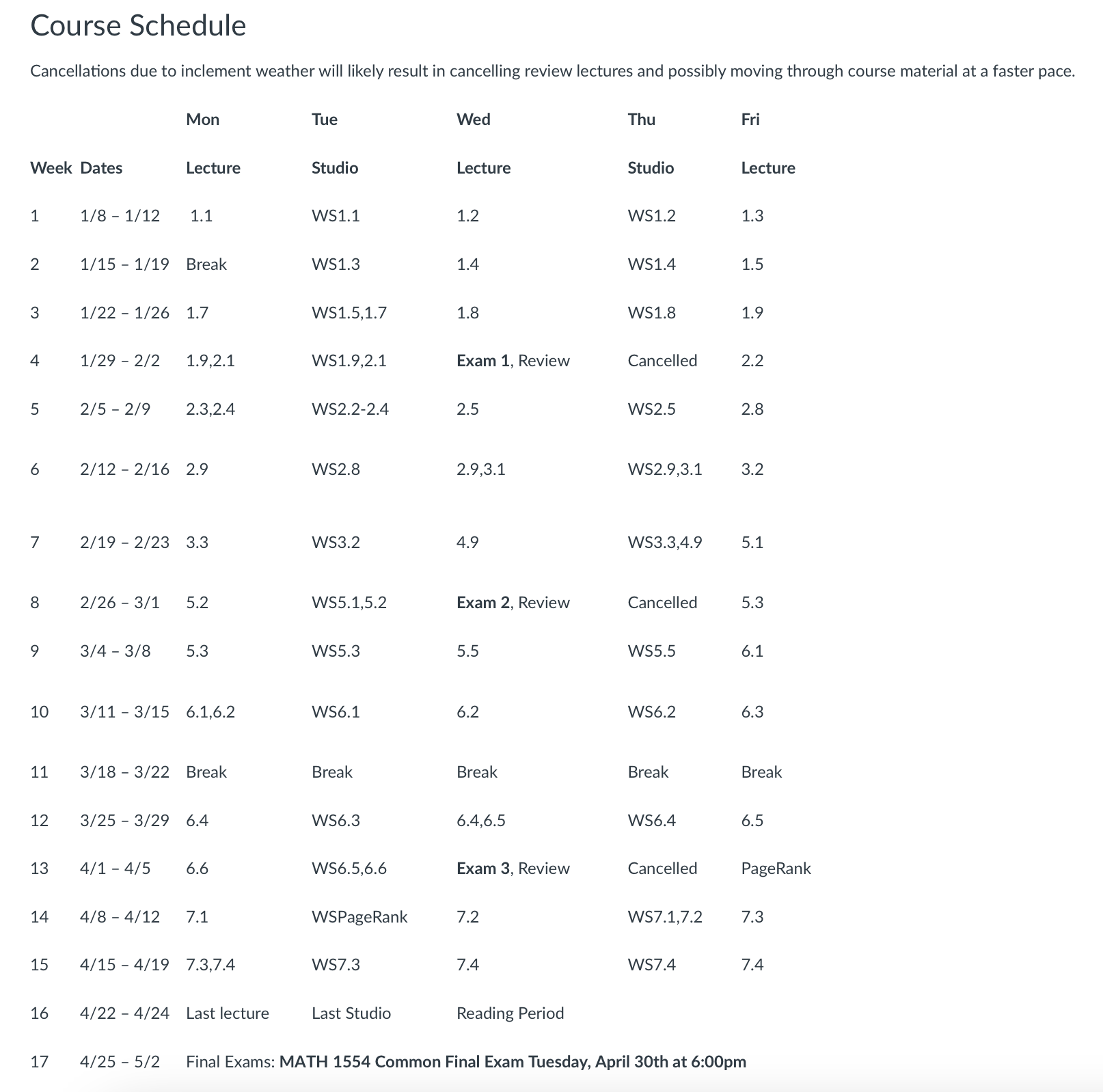
Week 1 - systems of linear equations, row reduction, echelon form, linear combination, spanWeek 2 - matrix equation, solution sets, parametric vector formWeek 3 - transformations, standard matrix, 1-to-1 and ontoWeek 4 - matrix multiplication, Exam 1 review, inverses, elementary matricesWeek 5 - inverses, IMT, partitioned matrices, LU decomposition, subspacesWeek 6 - basis and dimension, rank, determinants, cofactor expansion vs. row operationsWeek 7 - transformations and volume, Markov chains, regular stochastic matrix, eigenvectorsWeek 8 - eigenvalues, Exam 2 review, diagonalizationWeek 9 - Diagonalization, basis of eigenvectors, complex eigenvalues, dot product and orthogonalityWeek 10 - Orthonormal basis, orthogonal projection, four subspacesWeek 11 - Gram-Schmidt, QR decomposition, least squares, applications of least squaresWeek 12 - Least-squares with nonlinear models, Exam 3 review, PageRankWeek 13 - Symmetric matrices, orthogonal diagonalization, quadratic forms, constrained optimizationWeek 14 and 15 - SVDFinal Exam in-class review days <-- Updated 4/22!
Old Lecture Notes
Blank slides
Annotated Lecture Notes from Fall 2023
Week 1 - systems of linear equations, row reduction, echelon form, linear combination, spanWeek 2 - matrix equation, solution sets, parametric vector formWeek 3 - transformations, standard matrix, 1-to-1 and ontoWeek 4 - matrix multiplication, Exam 1 review, inverses, elementary matricesWeek 5 - inverses, IMT, partitioned matrices, LU decomposition, subspacesWeek 6 - basis and dimension, rank, determinants, cofactor expansion vs. row operations, transformations and volumeWeek 7 - Markov chains, regular stochastic matrix, eigenvectors and eigenvaluesWeek 8 - Exam 2 review, diagonalizationWeek 9 - Diagonalization, basis of eigenvectors, complex eigenvalues, dot product and orthogonalityWeek 10 - Orthonormal basis, orthogonal projection, four subspacesWeek 11 - Gram-Schmidt, QR decomposition, least squares, applications of least squaresWeek 12 - Least-squares with nonlinear models, Exam 3 review, PageRankWeek 13 - Symmetric matrices, orthogonal diagonalization, quadratic forms, constrained optimizationWeek 14 and 15 - SVDFinal Exam in-class review days
Annotated OneNote Lecture Slides Spring 2023
Lecture notes 9/13 (annotated)
Supplementary Material
Midterm Review Material
Old material
Review material from Fall 2019
Class Notes (from Spring '17 - but still awesome!)
Old Tests (for practice)
Important dates
Jan 8 First day of classes
Jan 15 MLK Day (No class)
Jan 31 Exam 1
Feb 12 Progress reports due
Feb 28 Exam 2
Mar 13 Drop Deadline/Withdrawal Deadline
Mar 18-22 Spring Break (No Class)
Apr 3 Exam 3
Apr 22-23 Last day of lecture/studio
Apr 24 Reading period (no exams)
Apr 30 FINAL EXAM (Common Exam Slot for 1554) 6pm
Studio Meeting Times
CRN COURSE Section Instructor (s)Days Time (start) Time (end) Building Room
27711
1554
J
Barone, Salvador
MWF
1400
1450
CollegeOfComputing
16
24895
1554
J01
Feng, Jingyi
TR
1530
1620
Skiles
156
24896
1554
J02
Omarov, Daniyar
TR
1530
1620
Skiles
168
24897
1554
J03
Feng, Jingyi
TR
1700
1750
Skiles
156
25321
1554
J04
Fullmer, Brennan
TR
1700
1750
Skiles
168
Web links
![[GaTech logo]](./logo.png)
![[GaTech logo]](./logo.png)